...A história das pipas possui mistérios, lendas, símbolos e mitos. Ela também encanta pela magia e beleza. Tudo deve ter começado quando o homem primitivo se deu conta de sua limitação diante da capacidade de voar dos pássaros. Essa frustração foi o mote para que ele desse asas a sua imaginação.
...Pipa, papagaio ou pandorga, entre outras denominações, pode ser definido como um brinquedo que voa preso a extremidade de uma linha ou barbante. Em geral, tem uma armação leve de bambu ou madeira, sobre a qual se estica uma folha de papel ou plástico.

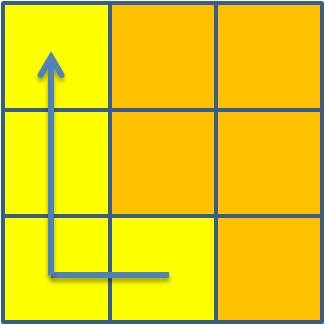
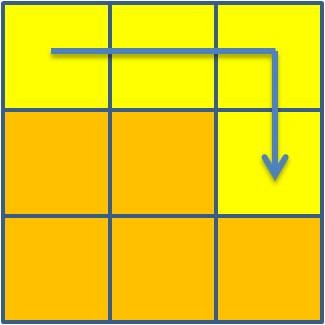
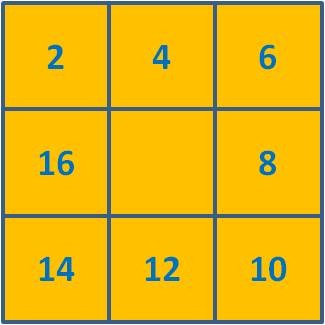
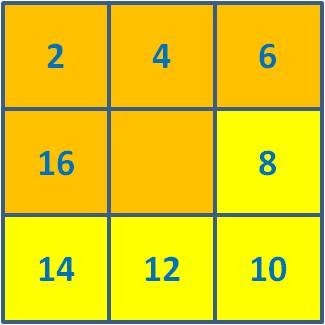
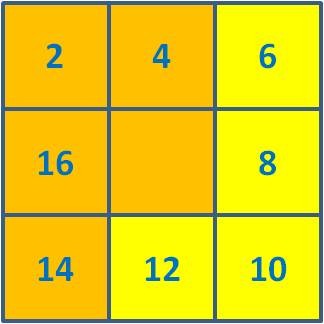
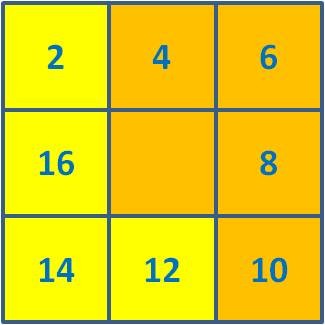
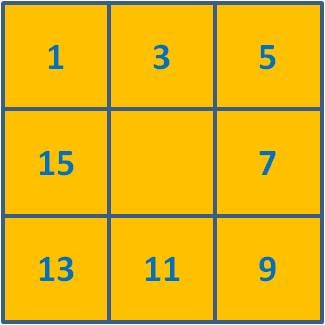
... A Pipa também ajuda na construção dos conceitos matemáticos. Com ela podemos ensinar a geometria de forma lúdica, desenvolvendo o raciocínio lógico sempre promovendo, nesta construção, a formação do indivíduo com um trabalho cooperativo onde há respeito pelo ambiente em que se vive. Durante a construção, a Pipa, é caracterizada por alguns entes geométricos como: linhas concorrentes, paralelas, triângulos, retângulos, triângulos retângulo, losangos, ângulos etc.
...Quem achar, contudo que as pipas não têm outra utilidade, a não ser diversão, engana-se. O milenar brinquedo auxiliou na criação do pára-raios, esteve presente na primeira transmissão radiofônica e ainda auxiliou Santos Dumont em suas primeiras experiências, entre outros atributos.

...Os historiadores acreditam que tenha sido inventada entre 400 e 300 (A.C.) por Arquitas, um grego da cidade de Tarena. Os chineses afirmam, contudo, que o general Han Sin a inventou em 206 (AC), para uso dos militares.
...Em 1749 o escocês Alexander Wilson usou vários termômetros presos as pipas para medir a temperatura nas alturas. Já Benjamim Franklin, em 1752, utilizando uma pipa forrada de pano, demonstrou em um dia de chuva, que nas nuvens existe eletricidade estática, criando assim o pára-raios.
...O inglês Douglas Archibasld, em 1883, prendeu um anemômetro (medidor de vento) à linha de uma pipa e mediu a velocidade do vento a 360m de altura. A aerofotografia com o auxílio de pipas também é muito praticada desde o fim do século XIX. Guglielmo Marconi em 1901 usou uma pipa para erguer uma antena e fez a primeira transmissão de rádio.
...No fim do século XIX e inicio do século XX, o homem estava decidido a construir uma máquina que lhe permitisse voar, nessa época ele só tinha duas referências de vôo, que eram as aves e a pipa. Muitos tentaram imitar os pássaros com suas máquinas sem sucesso, outros tentavam usando pipas.
...Em 1906, depois de vários testes, o brasileiro Alberto Santos Dumont fez o primeiro vôo, usando um conjunto de pipas-caixas, acionadas por suas próprias forças. Este avião recebeu o nome de “14 BIS”. Fonte: www.pipas.art.br
...Nós brasileiros conhecemos as pipas através dos colonizadores portugueses por volta de 1596 que, por sua vez, as conheceram através de suas viagens ao Oriente. Um fato pouco conhecido de nossa História deu-se no Quilombo dos Palmares, quando sentinelas avançadas anunciavam por meio de pipas quando algum perigo se aproximava mais uma prova de que a pipa era conhecida na África há muito mais tempo, pois os negros já cultuavam-na como oferenda aos deuses. http://www.pipas.com.br