À procura de regularidades

À procura de regularidades

Tem sido hábito neste blog eu suscitar a reflexão relativamente às múltiplas maneiras como os números se podem relacionar entre si. Muitas vezes essas relações são explícitas e evidentes, outras carecem de alguma investigação, suportada inicialmente apenas por intuição, intuição essa que acaba por gerar descoberta ou confirmação de relações matemáticas aparentemente inexistentes.

O exemplo que trago para ajudar a confirmar este segundo tipo de relações numéricas assenta na seguinte figura, constituídas pelos primeiros oito números naturais consecutivos:

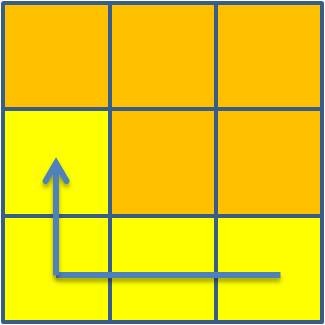
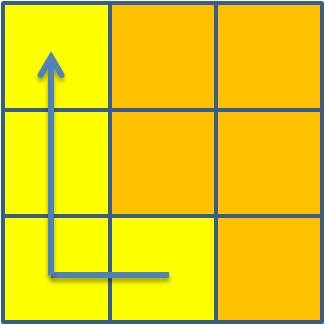
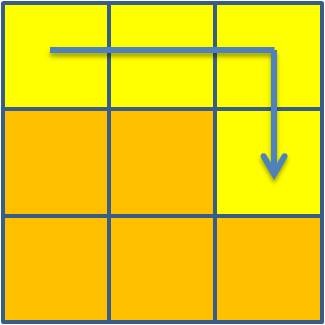
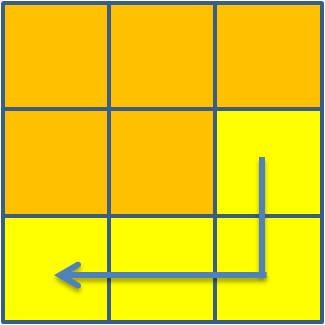
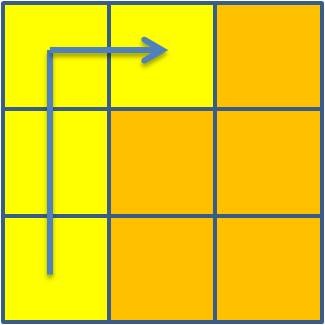
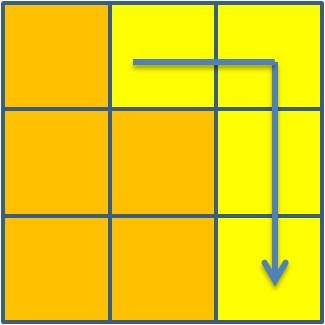
O objetivo é investigar se existe algum tipo de regularidade se se considerar, de cada vez, a soma de quatros desses números, de acordo com o esquema de análise seguinte:

  

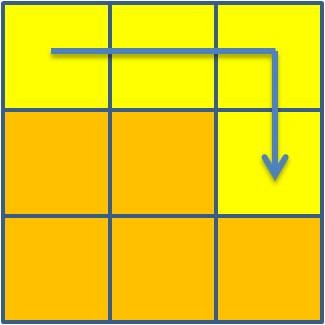 Vejamos cada caso: 

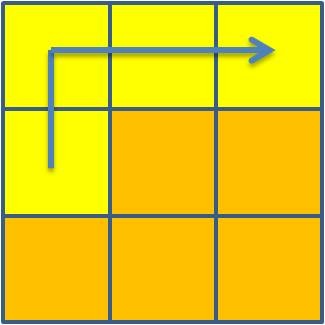
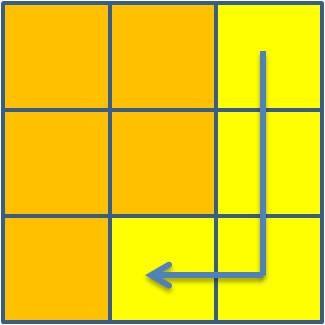
1 + 2 + 3 + 4 = 10	4 + 5 + 6 + 7 = 22	7 + 8 + 1 + 2 = 18
2 + 3 + 4 + 5 = 14	5 + 6 + 7 + 8 = 26	8 + 1 + 2 + 3 = 14
3 + 4 + 5 + 6 = 18	6 + 7 + 8 + 1 = 22	1 + 2 + 3 + 4 = 10

Curiosamente, se colocarmos as várias somas obtidas em linha, verificamos que existe uma regularidade numérica, pois o que acontece antes do valor central, volta a ocorrer a seguir a ele, num processo simétrico:

10     22     18     14     26     14     18     22     10

Se se substituírem os valores iniciais pelos seus respetivos dobros, o que é previsível que aconteça? Consegue antever a menor e a maior das somas?

Analisem-se, então, as várias figuras se a inicial for a seguinte:

As novas somas associadas às nove figuras respetivas são as seguintes: 

2 + 4 + 6 + 8 = 20	8 + 10 + 12 + 14 = 44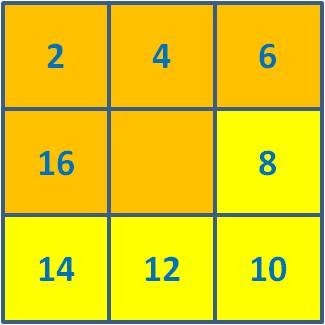	14 + 16 + 2 + 4 = 36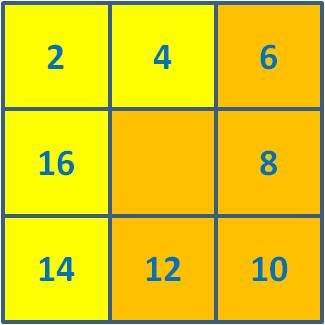
4 + 6 + 8 + 10 = 28	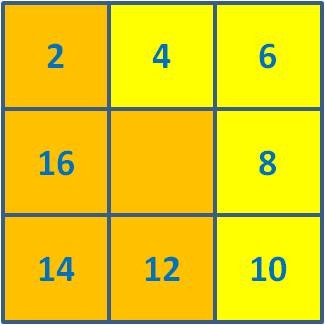10 + 12 + 14 + 16 = 52	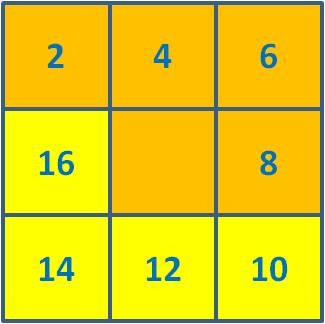16 + 2 + 4 + 6 = 28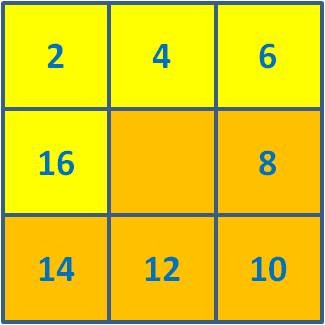
6 + 8 + 10 + 12 = 36	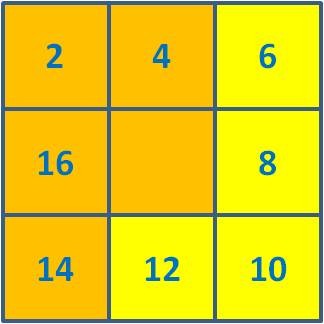12 + 14 + 16 + 2 = 44	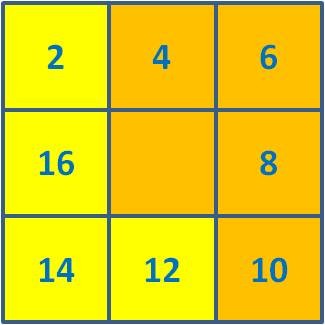2 + 4 + 6 + 8 = 20

Tal como, provavelmente, seria de prever, os valores de cada soma duplicam os respetivos valores de cada soma da tarefa anterior:

20     44     36     28     52     28     36     44     20  

Uma vez mais, constata-se a existência de uma regularidade de cariz simétrica, tendo em conta o valor central.

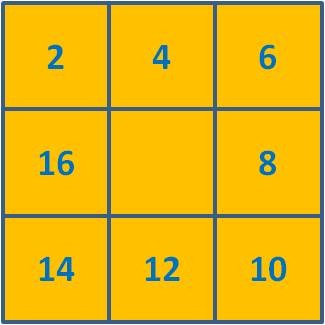
Note-se que estivemos a fazer com estudo envolvendo os primeiros oito números pares. O que ocorrerá se se comparar este estudo com um outro, envolvendo os primeiros oito números ímpares?

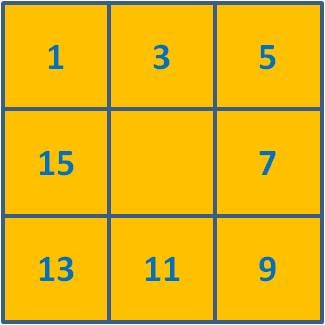
A figura inicial será a seguinte:

Consegue antecipar resultados? Com que fundamentação o faz?